ARIMA-MODELLE
Quelle: https://www.statistik-nachhilfe.de/ratgeber/statistik/induktive-statistik/statistische-modellbildung-und-weitere-methoden/zeitreihenanalyse/arima-modelle
In ARIMA-Modellen werden autoregressive Prozesse mit Moving Average (MA)-Prozessen kombiniert. Autoregressive (AR-)Modelle führen Beobachtungen zum Zeitpunkt nur auf die vergangenen Beobachtungen zurück. In Moving Average-Prozessen werden Beobachtungen jedoch nicht auf die Beobachtungen x, sondern auch auf den nicht-beobachteten Fehler \varepsilon der vergangenen Zeitperioden zurückgeführt, der ebenso einen Einfluss auf Deine zukünftigen Beobachtungen ausübt. Damit machst Du Dir in ARIMA-Modellen nicht nur die beobachteten, vergangenen Beobachtungen zunutze, sondern auch Informationen, die Du nicht direkt in Deiner Zeitreihe beschreibst, sondern als Fehler Deiner Vorhersage definierst.
MA-Prozesse sind besser darin, Abhängigkeiten in Deinen Beobachtungen zu modellieren, die kurz auftreten und sich dann wieder auflösen, während AR-Prozesse zeitliche Abhängigkeiten modellieren, die von Dauer über die Zeitreihe auftreten. Um herauszufinden, ob ein AR oder MA-Prozess vorliegt, hilft ein genauerer Blick auf die Autokorrelationsfunktion der Zeitreihe. Autokorrelationen können über ein Korrelogram der Zeitreihe mit sich selber bzw. ihren lags, also ihren verzögerten Wirkungen, beschrieben werden. Stellen wir eine Autokorrelation über mehrere lags fest, handelt es sich um einen autoregressiven Prozess, der Abhängigkeiten über die gesamte Zeitreihe berücksichtigen sollte. Stellen wir nur Abhängigkeiten für eine kurze Dauer fest, handelt es sich eher um einen MA-Prozess. Falls AR-Prozesse vorliegen, stellt sich die Frage, ob es sich um AR-Prozesse höherer Ordnung handelt, also ob es sich um Abhängigkeiten handelt, die zwar über die gesamte Zeitreihe, aber nicht nur von jeweiligen vergangenen Zeitpunkt, sondern auch von Zeitpunkten in der ferneren Vergangenheit abhängen. Dafür hilft ein Blick auf die partielle Autokorrelationsfunktion. Diese untersucht die Abhängigkeiten in der Zeitreihe, wenn die Abhängigkeit zum Zeitpunkt t-1 aufgelöst wird. Beobachten wir dann weitere Abhängigkeiten über den Zeitpunkt t-1 hinaus, solltest Du AR-Prozesse höherer Ordnung modellieren.
Die Voraussetzung für die Modellierung von AR- und MA-Prozessen ist, dass Deine Zeitreihe stationär ist. Das heißt, Deine Zeitreihe hat zu jeder Zeit den gleichen Mittelwert und die gleiche Varianz; Trends und unterschiedliche saisonale Effekte liegen in stationären Zeitreihen nicht (mehr) vor. Mit einfachen Worten könnte man auch sagen, Deine Zeitreihe ist gleichmäßig. In der Realität sind viele Zeitreihen aber nicht gleichmäßig, sondern verfolgen Trends oder Saisonalitäten, die unterschiedliche Mittelwerte und Varianzen über die Zeit zeigen. Zum Beispiel ist in der Regel die Varianz in den Verkäufen eines Unternehmens nicht regelmäßig und folgt einem gewissen Trend. Um nicht-stationäre oder ungleichmäßige Zeitreihen korrekt zu bestimmen, musst Du diese stationär machen. Dies ermöglichen ARIMA-Modelle – Autoregressive Integrated Moving Average-Modelle. In ARIMA-Prozessen werden Trends in Zeitreihen über Differenzierung integriert und dadurch stationär. Das heißt, der Mittelwert Deiner Beobachtungen wird konstant, indem Dein Outcome, bspw. Deine Verkäufe y zum Zeitpunkt t-k von y zum Zeitpunkt t subtrahiert werden. Es kann genauso sein, dass die Varianz Deiner Beobachtungen nicht stationär ist, sodass y mithilfe des natürlichen Logarithmus stationär transformiert werden kann. Genauso sind natürliche, andere Transformationen der Zeitreihe möglich, um stationäre Zeitreihen sicherzustellen.
Zusammengefasst kombinieren ARIMA-Modelle AR-Modelle und MA-Prozesse folgendermaßen:
\[y_t=\alpha +\ {\emptyset }_1y_{dt-1}+{\emptyset }_py_{dt-p}+{\theta }_1{\varepsilon }_{t-1}+{\theta }_q{\varepsilon }_{t-q}+{\varepsilon }_t\]
y_d sind dabei Deine d-fach differenzierten Beobachtungen, die einem AR-Prozess mit p Ordnungen und einem MA-Prozess mit q Ordnungen folgen können. Deine Aufgabe ist es daher die Parameter d, also die Ordnung der notwendigen Integration bzw. Differenzierung, sowie p und q in Deinem ARIMA (p,d,q)-Modell zu spezifizieren.
Stell Dir zum Beispiel vor, Du analysierst Deine Verkäufe in Deinem Online-Shop seit Gründung vor 5 Jahren im Jahre 2013 und stellst fest, dass Dein Geschäft mit jedem Jahr besser läuft. Ein Ausschnitt Deiner monatlichen Verkaufszahlen im Jahre 2017 sieht folgendermaßen aus:
Monat 1/17 2/17 3/17 4/17 5/17 6/17 7/17 8/17 9/17 10/17 11/17 12/17
Verkäufe 196 196 236 235 229 243 264 272 237 211 189 201
Der Verlauf Deiner Verkäufe zeigt Dir jedes Jahr zwei Verkaufsspitzen. Im Frühjahr und im Sommer hast Du relativ stark steigende Verkäufe, die daraufhin wieder genauso stark fallen. Du willst nun herausfinden, wie sich Deine Verkäufe im kommenden Jahr entwickeln werden. Du erkennst in Deiner Zeitreihe, dass Deine Verkäufe keinem zufälligen Verlauf folgen, sondern erkennst einen klaren Trend mit saisonalen Effekten. Einen solchen Verlauf kannst Du gut mithilfe eines ARIMA-Modells beschreiben. Deine Autokorrelationsfunktion bestätigt, dass Du im Frühjahr und im Sommer jeweils einen starken Monat hast, nach dem Deine Verkäufe wieder abfallen. Deine Verkäufe folgen keinem AR-Prozess, sondern einem MA(1)-Prozess. Du berücksichtigst den Trend in Deinen Verkäufen, indem Du die Daten zur ersten Ordnung differenzierst. Damit hast Du alle Parameter deines Modells bestimmt. Dein Modell folgt keinem AR-Prozess, sondern einem MA(1)-Prozess, den Du zur ersten Ordnung integrierst. Du bestimmst also ein ARIMA(0,1,1)-Modell. Die ungleiche Varianz begegnest Du noch mit einer Log-Transformation der Daten, sodass Du den Verlauf einer stationären Zeitreihe korrekt schätzen kannst. Der untenstehende Graph Deiner Verkäufe zeigt Dir Deine tatsächlichen Verkäufe der letzten 5 Jahre zwischen 2013 und 2018 (schwarze Linie). Du erkennst auch, dass Du Deine Verkäufe über Dein ARIMA(0,1,1) gut spezifizieren konntest. Die Schätzung Deiner Verkäufe (rote Linie) folgt relativ gut Deinen tatsächlichen Verkäufen. Du schätzt Deine Verkäufe mithilfe Deines ARIMA(0,1,1)-Modells nun für das kommende Jahr und stellst fest (gestrichelte Linie), dass sich Dein Aufwärtstrend in Deinen Verkäufen fortsetzen und auch die saisonalen Effekte im Frühjahr und Sommer mit Wahrscheinlichkeit (nicht dargestellt) wiederholen werden.
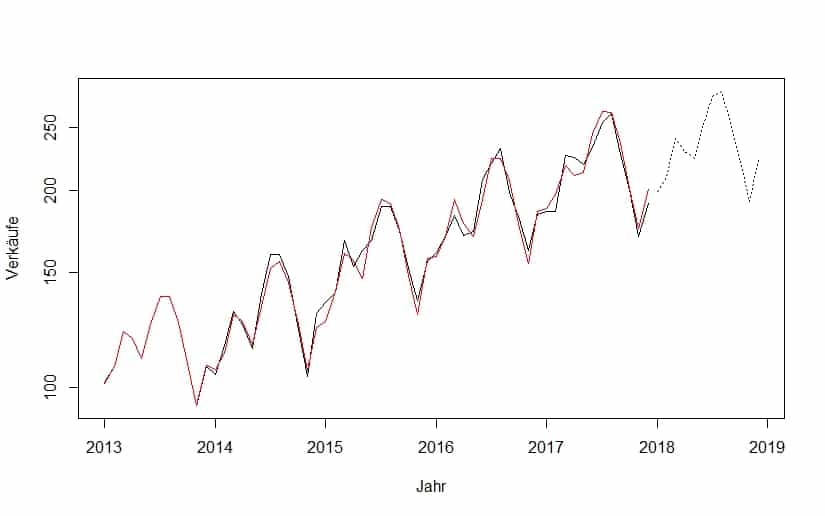
Obige Graphik zeigt die Anwendung des ARIMA-Modells auf die Umsatzentwicklung eines Einzelhandelsgeschäftes. Hier typisch für den Verlauf die Umsatzspitzen im Frühjahr (Ostergeschäft) und im Sommer, sowie die jeweils tiefen Einbrüche im Herbst bzw. dem beginnenden Winter.
- Schwarze Linie: Der tatsächliche Verlauf der Umsätze in der Vergangenheit
- Rote Linie: Die Anwendung des ARIMA-Modells auf die statistische Spezifizierung der Vergangenheit
- Gestrichelte Linie: Prognose der Umsatzentwicklung für ein Jahr mit diesem ARIMA-Modell
